L.C.M of Numbers
Table of Content:
L.C.M of Numbers
The Least Common Multiple (LCM) of two or more numbers is the smallest number that is a multiple of all the numbers.
For example, the LCM of 4 and 6 is 12, since 12 is the smallest number that is a multiple of both 4 and 6.
Factorization Method of Finding L.C.M.
The easiest and most common way to find the L.C.M of two numbers is by using the factorization method. In this method, we factorize the given numbers and identify the common factors. We then multiply all the common factors to get the L.C.M.
Example: Find the L.C.M. of 12 and 18
Solution:
12 = 2 x 2 x 3
18 = 2 x 3 x 3
Common Factors: 2 x 3
L.C.M = 2 x 3 x 2 x 3 = 36
Common Division Method of Finding L.C.M.
To find the Least Common Multiple (L.C.M.) of a set of numbers, the Common Division Method (Short-cut Method) can be used. Arrange the given numbers in any order and divide each by a number which is a factor of at least two of the numbers. Continue doing this until no two numbers can be divided by the same number, except for 1. The product of all the divisors and the remaining numbers is the L.C.M. of the set.
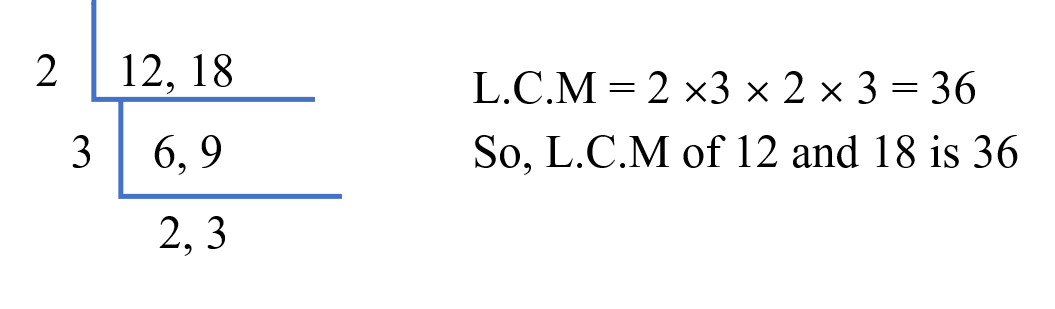
The formula for calculating the LCM and HCF of two numbers is:
\begin{equation} LCM = \frac{a \times b}{HCF} \end{equation} \begin{equation} HCF = \frac{a \times b}{LCM} \end{equation} \begin{equation} \\ Product \: of \: two \: numbers = Product \: of \: their \: H.C.F. \: and\: L.C.M. \end{equation} where a and b are the two numbers for which the LCM and HCF are to be calculated.The H.C.F. of two numbers is 11 and their L.C.M. is 693. If one of the numbers is 77, find the other.
\begin{align} \begin{split} \\ HCF &= 11. \\ LCM &= 693, \\ a &= 77. \\ Now, we \: know \: that, \\ Product \: of \: two \: numbers &= Product \: of \: their \: H.C.F. \: and\: L.C.M. \\ a \times b &= HCF \times LCM \\ b &= \frac{HCF \times LCM} {a} \\ b &= \frac{11 \times 693} {77} = 99 \end{split} \end{align}