H.C.F of Numbers
Table of Content:
Factors and Multiples
Factors: Factors are numbers that divide into a given number with no remainder.
Multiples: Multiples are numbers that a given number is a multiple of. Multiples are created by multiplying a number by any other number.
The Highest Common Factor (HCF)
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of the numbers exactly. It is also known as the Greatest Common Divisor (GCD).
Let's take two numbers, a = 12 and b = 18. The HCF of these two numbers can be found by dividing 12 by 18 until the remainder is zero.
\begin{equation} HCF(12, 18) = 6 \end{equation}There are two methods of finding the H.C.F. of a given set of numbers:
1. Factorization Method
2. Division Method
-
Factorization Method: Express each number as a product of its prime factors and find the common prime factors. The H.C.F is the product of the common prime factors.
-
Division Method: Keep dividing the largest number by the smaller number until the remainder is zero. The H.C.F is the last non-zero remainder.
Finding the H.C.F. of two numbers: The HCF of two numbers can be found by dividing the larger number by the smaller number until the remainder is zero.
Finding the H.C.F. of more than two numbers: Suppose we have to find the H.C.F. of three numbers. Then, H.C.F. of [(H.C.F. of any two) and (the third number)] gives the H.C.F. of three given numbers. Similarly, the H.C.F. of more than three numbers may be obtained.
Here's an example of how to use each method to find the H.C.F of the numbers 36 and 60:
-
Factorization Method:
a. Factorize 36 into prime factors: \( 36 = 2^2 * 3^2 \)
b. Factorize 60 into prime factors: \( 60 = 2^2 * 3 * 5 \)
c. The common prime factors of 36 and 60 are 2^2 and 3, so H.C.F = \( 2^2 * 3 = 12\) -
Division Method:
a. Divide the larger number (60) by the smaller number (36): \( 60 ÷ 36 = 1\) with a remainder of 24
b. Replace the larger number (60) with the smaller number (36) and the smaller number (36) with the remainder (24): 36 ÷ 24 = 1 with a remainder of 12
c. Replace the larger number (36) with the smaller number (24) and the smaller number (24) with the remainder (12): 24 ÷ 12 = 2 with a remainder of 0
d. The last non-zero remainder is 12, so the H.C.F = 12.

Division Method Example
Find the H.C.F of 513, 1134 and 1215
H.C.F of 1134 and 1215 is 81
So required H.C.F = H.C.F of 513 and 81
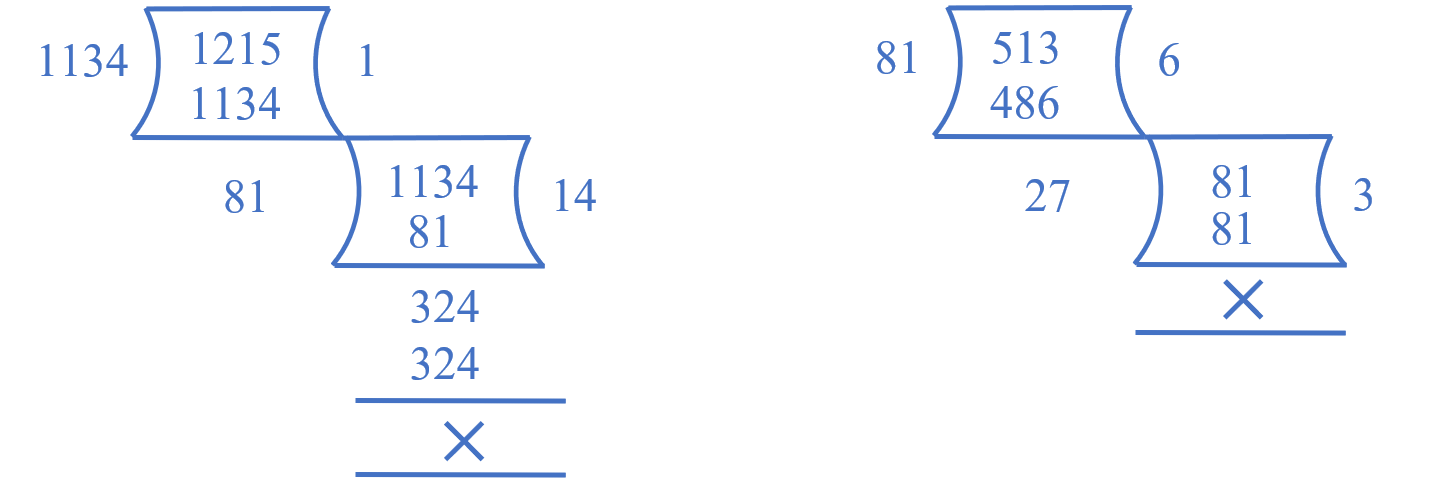
H.C.F of given numbers = 27