---

Merge sort is a sorting technique based on divide and conquer technique. With worst-case time complexity being ?(n log n), it is one of the most respected algorithms.

Merge Sort follows the rule of Divide and Conquer to sort a given set of numbers/elements, recursively, hence consuming less time.

Before jumping on to, how merge sort works and it's implementation, first let's understand what is the rule of Divide and Conquer?

Divide and Conquer

If we can break a single big problem into smaller sub-problems, solve the smaller sub-problems and combine their solutions to find the solution for the original big problem, it becomes easier to solve the whole problem.

Let's take an example, Divide and Rule.

When Britishers came to India, they saw a country with different religions living in harmony, hard-working but naive citizens, unity in diversity, and found it difficult to establish their empire. So, they adopted the policy of Divide and Rule. Where the population of India was collectively one big problem for them, they divided the problem into smaller problems, by instigating rivalries between local kings, making them stand against each other, and this worked very well for them.

Well, that was history, and a socio-political policy (Divide and Rule), but the idea here is, if we can somehow divide a problem into smaller sub-problems, it becomes easier to eventually solve the whole problem.

In Merge Sort, the given unsorted array with n elements, is divided into n subarrays, each having one element, because a single element is always sorted in itself. Then, it repeatedly merges these subarrays, to produce new sorted subarrays, and in the end, one complete sorted array is produced.

The concept of Divide and Conquer involves three steps:

1. Divide the problem into multiple small problems.
2. Conquer the subproblems by solving them. The idea is to break down the problem into atomic subproblems, where they are actually solved.
3. Combine the solutions of the subproblems to find the solution of the actual problem.

Divide and Conquer Strategy

Using the Divide and Conquer technique, we divide a problem into subproblems. When the solution to each subproblem is ready, we 'combine' the results from the subproblems to solve the main problem.

Suppose we had to sort an array A. A subproblem would be to sort a sub-section of this array starting at index p and ending at index r, denoted as A[p..r].

Divide

If q is the half-way point between p and r, then we can split the subarray A[p....r] into two arrays A[p,q] and A[q+1, r].

Conquer

In the conquer step, we try to sort both the subarrays A[p,q] and A[q+1, r]. If we haven't yet reached the base case, we again divide both these subarrays and try to sort them.

Combine

When the conquer step reaches the base step and we get two sorted subarrays A[p..q] and A[q+1, r] for array A[p....r], we combine the results by creating a sorted array A[p....r] from two sorted subarrays A[p,q] and A[q+1, r]

The MergeSort Algorithm

The MergeSort function repeatedly divides the array into two halves until we reach a stage where we try to perform MergeSort on a subarray of size 1 i.e. p == r.

After that, the merge function comes into play and combines the sorted arrays into larger arrays until the whole array is merged.

MergeSort(A, p, r)
    If p > r 
        return;
    q = (p+r)/2;
    mergeSort(A, p, q)
    mergeSort(A, q+1, r)
    merge(A, p, q, r)

To sort an entire array, we need to call MergeSort(A, 0, length(A)-1).

As shown in the image below, the merge sort algorithm recursively divides the array into halves until we reach the base case of array with 1 element. After that, the merge function picks up the sorted sub-arrays and merges them to gradually sort the entire array.

The merge step of merge sort

Every recursive algorithm is dependent on a base case and the ability to combine the results from base cases. Merge sort is no different. The most important part of the merge sort algorithm is, you guessed it, the "merge" step.

The merge step is the solution to the simple problem of merging two sorted lists(arrays) to build one large sorted list(array).

The algorithm maintains three-pointers, one for each of the two arrays and one for maintaining the current index of final sorted array.

Have we reached the end of any of the arrays?
    No:
        Compare current elements of both arrays 
        Copy smaller element into sorted array
        Move pointer of element containing smaller element
    Yes:
        Copy all remaining elements of non-empty array

How Merge Sort Works?

As we have already discussed that merge sort utilizes divide-and-conquer rule to break the problem into sub-problems, the problem in this case being, sorting a given array.

In merge sort, we break the given array midway, for example, if the original array had 6 elements, then merge sort will break it down into two subarrays with 3 elements each.

But breaking the orignal array into 2 smaller subarrays is not helping us in sorting the array.

So we will break these subarrays into even smaller subarrays until we have multiple subarrays with a single element in them. Now, the idea here is that an array with a single element is already sorted, so once we break the original array into subarrays which has only a single element, we have successfully broken down our problem into base problems.

And then we have to merge all these sorted subarrays, step by step to form one single sorted array.

Let's consider an array with values {14, 7, 3, 12, 9, 11, 6, 12}

Below, we have a pictorial representation of how merge sort will sort the given array.

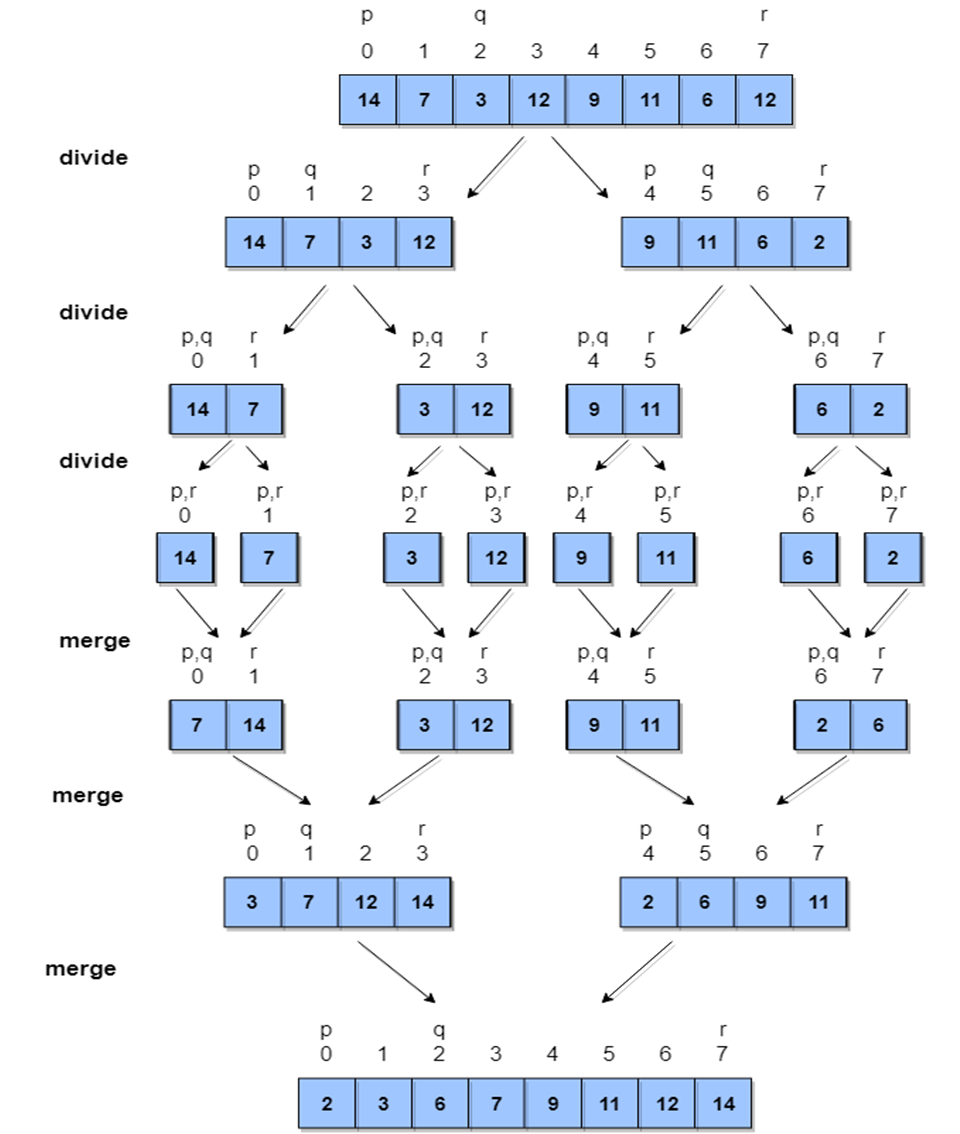
In merge sort we follow the following steps:

1. We take a variable p and store the starting index of our array in this. And we take another variable r and store the last index of array in it.
2. Then we find the middle of the array using the formula (p + r)/2 and mark the middle index as q, and break the array into two subarrays, from p to q and from q + 1 to r index.
3. Then we divide these 2 subarrays again, just like we divided our main array and this continues.
4. Once we have divided the main array into subarrays with single elements, then we start merging the subarrays.

Writing the code for merge algorithm

A noticeable difference between the merging step we described above and the one we use for merge sort is that we only perform the merge function on consecutive sub-arrays.

This is why we only need the array, the first position, the last index of the first subarray(we can calculate the first index of second subarray) and the last index of second subarray.

Our task is to merge two subarrays A[p..q] and A[q+1..r] to create a sorted array A[p..r]. So the inputs to the function are A, p, q and r 

The merge function works as follows:

1. Create copies of the subarrays L ? A[p..q] and M ? A[q+1..r].
2. Create three pointers i,j and k
   1. i maintains current index of L, starting at 1
   2. j maintains current index of M, starting at 1
   3. k maintains current index of A[p..q], starting at p
3. Until we reach the end of either L or M, pick the larger among the elements from L and M and place them in the correct position at A[p..q]
4. When we run out of elements in either L or M, pick up the remaining elements and put in A[p..q]

In code, this would look like:

Assune that index start with 1

void merge(int A[], int p, int q, int r)
{
    /* Create L ? A[p..q] and M ? A[q+1..r] */
    int n1 = q - p + 1;
    int n2 =  r - q;
 
    int L[n1], M[n2];

    for (i = 1; i < n1; i++)
        L[i] = A[p + i-1];
    for (j = 1; j < n2; j++)
        M[j] = A[q + j];
		
		
	L[n1+1]=Infinity
    M[n2+1]=Infinity	
    
    /* Maintain current index of sub-arrays and main array */
    int i, j, k;
    i = 1; 
    j = 1; 
    k = p; 
	
	
	for(k=p to r)
	
	if(L[i]<= M[j])
	  A[k] = L[i]
	  i = i+1;
	  
	 else
      A[k] = M[j]
	  j = j+1; 

In code, this would look like: Assume that index start with 0

void merge(int A[], int p, int q, int r)
{
    /* Create L ? A[p..q] and M ? A[q+1..r] */
    int n1 = q - p + 1;
    int n2 =  r - q;
 
    int L[n1], M[n2];

    for (i = 0; i < n1; i++)
        L[i] = A[p + i];
    for (j = 0; j < n2; j++)
        M[j] = A[q + 1 + j];
    
    /* Maintain current index of sub-arrays and main array */
    int i, j, k;
    i = 0; 
    j = 0; 
    k = p; 


    /* Until we reach either end of either L or M, pick larger among elements L and M and place them in the correct position at A[p..r] */
    while (i < n1 && j < n2)
    {
        if (L[i] <= M[j])
        {
            arr[k] = L[i];
            i++;
        }
        else
        {
            arr[k] = M[j];
            j++;
        }
        k++;
    }
 
    /* When we run out of elements in either L or M, pick up the remaining elements and put in A[p..r] */
    while (i < n1)
    {
        A[k] = L[i];
        i++;
        k++;
    }
 
    while (j < n2)
    {
        A[k] = M[j];
        j++;
        k++;
    }
}

Merge function explained step-by-step

There is a lot happening in this function, so let's take an example to see how this would work.

As usual, a picture speaks a thousand words.

The array A[0..8] contains two sorted subarrays A[1..5] and A[6..7]. Let us see how merge function will merge the two arrays.

	  
void merge(int A[], int p = 1, int q = 4, int 6)
{
	  

Step 1: Create duplicate copies of sub-arrays to be sorted

  /* Create L ? A[p..q] and M ? A[q+1..r] */
    n1 = 4 - 1 + 1 = 4;
    n2 =  6 - 4 = 2;
 
    int L[4], M[2];

    for (i = 0; i < 4; i++)
        L[i] = A[p + i];
    /* L[0,1,2,3] = A[1,2,3,4] = [1,5,10,12] */

    for (j = 0; j < 2; j++)
        M[j] = A[q + 1 + j];
    /* M[0,1,2,3] = A[5,6] = [6,9] 

Step 2: Maintain current index of sub-arrays and main array

    int i, j, k;
    i = 0; 
    j = 0; 
    k = p;  

Step 3: Until we reach end of either L or M, pick larger among elements L and M and place them in the correct position at A[p..r]

    while (i < n1 && j < n2) { 
        if (L[i] <= M[j]) { 
            A[k] = L[i]; i++; 
        } 
        else { 
            A[k] = M[j]; 
            j++; 
        } 
        k++; 
     

Step 4: When we run out of elements in either L or M, pick up the remaining elements and put in A[p..r]

/* We exited the earlier loop because j < n2 doesn't hold */  
    while (i < n1)
    {
        A[k] = L[i];
        i++;
        k++;
    }

/* We exited the earlier loop because i < n1 doesn't hold */  
 
    while (j < n2)
    {
        A[k] = M[j];
        j++;
        k++;
    }
}

This step would have been needed if size of M was greater than L.

At the end of the merge function, the subarray A[p..r] is sorted.

---